Initially the cannon falls along the slope a distance of l and along this process it falls a height
and so loose a potential energy of 
. This loss in potential energy is converted into kinetic energy. Suppose that the velocity of the cannon along the slope just before firing the cannon ball is v then,
When the cannon shoots the cannon ball, suppose that it exerts a force F(t) on the cannon ball (this can be some arbitrary function) in order to accelerate it while shooting. The cannon ball in turn as a reaction exerts the same force F(t) on the cannon pushing it towards the inclined plane. Hence during the time when the cannon ball is being shot, there are two forces acting on the cannon, i) the reaction from the cannon ball F(t) and ii) the force of gravity Mg acting downwards. The equation of motion to determine the deceleration a(t) of the cannon along the slope is then given by,
The velocity of the cannon at a time t during the brief shooting period is given by,
The only force acting on the cannon ball accelerating it is the force F(t). Suppose that the momentum of the cannon ball at time t is P(t), then,
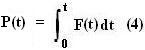
From (3) and (4) we have,
Suppose that the duration of the shot is T. We know that the cannon stopped after firing, which means that Vf(T)=0. Also the final momentum of the the cannon ball is P, so P(T)=p. in other words,
