Irodov Problem 1.187

The instantaneous angular momentum of the particle with respect to a point O', is given by 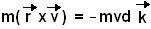as shown in the figure beside. Here d is the distance of the point O' from the straight line L that passes through the the velocity vector of the particle (given by length of O'P the perpendicular from O' on line L). The angular momentum will always be directed perpendicular to the plane of the position and velocity vectors, i.e. along the z-axis (k is the unit vector directed in the positive z direction i.e. coming out of the surface towards you). The negative sign in the above expression comes because the angular momentum vector will be directed along the negative z direction i.e into the surface (using the Ambrose Flemings right hand rule for cross product).

In order for the angular momentum to not change even after reflection, since the magnitude of velocity does not change, the distance of the point O' from the velocity vector of the particle before and after the reflection must not change.
In the figure thus, all the points O' that satisfy the condition d1 = d2 or O'P1 = O'P2. This condition holds true only for all the points that are equidistant from both lines L1 and L2 i.e that lie on the angle bisector of line L1 and L2.


An alternative intuitive explanation

Torque is responsible to change the angular momentum of a particle. In order for the particles angular momentum not to change before and after collision the particle should not experience any torque with respect to point O' during the collision with the wall. During the collision from the wall the particle will experience a normal reaction force, that is responsible for changing its direction of motion. This same normal reaction will also be responsible for generating the torque on the particle in order for its angular momentum to change. If O' is so chosen that the torque generated by the Normal reaction as seen from O' is 0, then the angular momentum of the particle will not change. Since Normal reaction is not 0, the only way the torque can be zero is if the direction of normal reaction passes through point O' to make the moment arm 0. In other words, O' must lie on the normal to the plane of reflection passing through the point of reflection.


b)
As seen in the figure, the distances of point O' from the trajectories (line passing through the velocity vector) of the particle before and after reflection
is given by O'P1 = O'P2 = .

The angular momentum of the particle before reflection as seen from O' is given by . The negative sign comes because the angular momentum vector will be direction into the surface as obtain by using Flemings right hand rule for cross product.


After reflection the magnitude of the angular momentum of the particle does not change but its direction flips (also obtained by using Flemings right hand rule) and is given by . The change in angular momentum is thus given by,