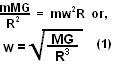Irodov Problem 1.226

The satellite is moving very close to the Earth's surface, so we can assume that the radius of its orbit is almost equal to R - the radius of the Earth. Let the mass of Earth be M and its time period of rotation about its own axis be T. As already solved in problem 1.225, the angular velocity of the satellite w with respect to a stationary observer is given by irrespective of the direction (East to West or West to East) it moves. It absolute velocity is given by . The absolute velocity of an observer on Earth is given by . The velocity of the satellite as measured by an observer on Earth for the two satellites (moving East to West and West to East) will be v+vE and v-vE respectively. So the ratio of kinetic energies of the satellite (of mass m ) as perceived by an observer on Earth will be,









The exact numerical value can be computed by putting the values,



given by approximately 1.27.

Irodov Problem 1.225

Suppose that the angular velocity of the satellite w.r.t. to the axis of rotation of the Earth is w and that of Earth is wE.
The gravitational force experienced by the satellite is given by and its centripetal acceleration is given by . So we have,



Now the observer fixed to the rotating frame of the Earth is rotating along with the Earth West to East with angular velocity wE, while the satellite moves East to West with angular velocity w. The angular velocity of the satellite as seen by the observer fixed to the rotating axis of Earth wo will be w + wE. So we have,



The velocity of the satellite as seen by an observer who rotates with the Earth and is located at its center is given by,

Irodov Problem 1.224

Let w be the satellites angular velocity w.r.t the axis of rotation of Earth and let wE be the Earth's angular velocity.
Earth rotates from West to East (since sun rises in the East and sets in the West). The satellite is also moving from West to East i.e. in the same direction as that of Earth's rotation about its axis. The angular velocity seen by an observer wo on the Earth will thus be w-wE. Thus, we have,

The force of gravity at the satellite is acting radially inwards, its centripetal acceleration is . The mass of the satellite being m and M is the mass of the Earth. So we have,