Since, gravity acts vertically downwards, it does not effect the horizontal components of velocities of P1 and P2. However, both P1 and P2 accelerate at equal rates of g downwards from zero initial velocity component downwards.
The velocity of P1 after time t is given by
 and that of P2 is given by
and that of P2 is given by  . When the two velocity vectors are perpendicular to each other, the dot product of the vectors will be null, i.e.
. When the two velocity vectors are perpendicular to each other, the dot product of the vectors will be null, i.e.
The vertical distance traveled by the P1 and P2 will be identical, thus at any time t the distance between the two particles is only a function of the horizontal components of their positions given by, (v1 + v2)t. Thus, the distance between the two particles when their velocity vectors are mutually perpendicular are given by,
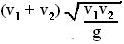
10 comments:
Thanks a Lot for putting it up..It really helps us a hell lot..... - debarati-
great work
jatin bisht
Thanks, you solution was simple and neat.
thanks dude ...............very helpful!
Job well done
I have never seen such gr8 solution.
By the way this really helps me a lot.
A lot lot lot lot lot.
Thanks a lot.
Thanks .now I think I am grasping kinematics
VERY NICE SOLUTIONS
A VERY SIMPLE SOLUTION WHICH ONE CAN EASILY UNDERSTAND.THANKS A LOT
Simply great
Post a Comment