Here the boats speed is less than that of the river, so there is no way that the boat can move in a direction perpendicular to the flow - thus there will be a drift. Suppose that the boat travels at an angle 
to the perpendicular direction as shown in the figure. Further suppose that the boat speed is v and the river speed is u. Then, the boat will travel at a speed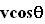 
towards the bank. Thus, if the river is x units wide it will take 
time for the boat to reach the other shore. During this entire time however, the boat is drifting with the river with a speed 
. Thus, the drift will be,
.
This drift will be minimized when,
It is trivial to show that the second derivative is positive at this value indicating that the value obtained is indeed a minima.
3 comments:
Hi Krishna
Thanks for the solution, but I have few questions.
1. Why do you think there will be a drift even though the boat has velocity component Vsin@. I mean Vsin@ can be such that it is equal to velocity of water.
2. The question says that "A boat moves relative to the water with a velocity which is n=2 times less than the river flow velocity". This means that if river speed (with respect to the ground) is V, then the speed of the boat (with respect to the water) is V/n. But I don't see that the solution resolves this ratio in terms of velocities w.r.t ground.
Ans 1. since sin@ is always less than 1, and V (boat velocity) is less than u (river velocity), Vsin@ will always be less than u. So drift cannot be avoided. This is explained in the first few lines of the solution.
Ans 2. In the solution v is velocity of the boat relative to the water and the velocity of the water is u, this is why the net drift w.r.t stationary frame of reference is u-vcos@.
I hope this clarifies your questions.
-krishna
Thanks for taking time to explain. I understood the Ans 1. It does actually makes sense.
I still can't understand the Ans2. I think velocity of boat w.r.t ground should be equal to velocity of boat w.r.t to water + velocity of water.
Is that what you are calling net drift w.r.t stationary observer?
BTW what kind of tool do you use to create these answers? The reason I ask is that most of the math shown are in form of images.
Thanks once again.
Post a Comment