The force diagrams for each of the three bodies is depicted in the figure beside.Forces on
:The tension in the string pulls the mass upwards while the gravitational force pulls it downwards and the net acceleration is w. Thus,
Forces on
:In the vertical direction there are two forces - the normal reaction from the surface and the force of gravity pulling it down. However, there is no downward acceleration for the body. Thus,
we have,Now in the vertical direction there are three forces acting on the mass, the tension from the two strings on either sides of the mass pulling the it in opposite directions (as shown in the figure) and the force of friction that is given by
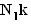in a direction so as to oppose any motion (the acceleration). Further the mass moves with an acceleration w. Thus, we have,
Forces on
:In the vertical direction there are two forces acting on mass
- the normal reaction from the surface acting upwards and the force of gravity acting downwards. There is no acceleration for this mass in the vertical direction. Thus, we have,
In the horizontal direction there are two forces acting on the mass - the tension in the string and the force of friction. The mass accelerates at a rate w. Thus, we have,
Now, we can solve for w as below,
Now we can use (9) and (7) to obtain the value of the tension
between the masses as,
4 comments:
Why will we take different tension for mo and m1.m2
There are two different strings and hence will in general have different tensions.
if the tensions are different then the acceleration should also be different???
The accelerations must be the same to ensure that the strings are not slackened
even though the tensions in the strings are different the accelerations will be different ... for two reasons, i) for one mass both string tensions are pulling in opposite directions for the other only one string is pulling it
ii) the masses are also different
Post a Comment