Irodov Problem 1.72

The force diagram of the problem is shown beside. We assume that that the masses are

and

, the tensions in the two strings are

and

and their accelerations are

and

respectively. This is indicated in the figure.

Now let us consider the relavent forces acting on each of the two masses first.

Forces acting on mass

: For this problem we need to only consider forces acting on the body1 along a direction parallel to the inclined plane . There are two forces along this direction - i) the component of force of gravity

and ii) the tension in the string

, as shown in the figure. The mass accelerates up the inclined plane at a rate

. Thus the equation of motion for body 1 can be written as,

Forces acting on mass

: There are two forces acting on this mass, i) the tension

in the second string and the force of gravity

as shown in the figure. Since we have assumed that body 1 is moving up the plane, the reasonable thing is to assume that body 2 moves down. Suppose that it moves down

with an acceleration of

. Its dynamics are given as,

Forces on the Moving Pulley holding

: There are three forces acting on the pulley, i) the tensions

acting to pull the pulley down from each part of the thread that holds

and ii) the tension

in the thread holding mass

. The mass of he pulley is 0 and it will accelerate at a rate

downwards. Thus, we can write the dynamics of the pulley as,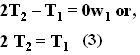

How are

and

related ?: There is one more piece needed to solve the problem, the fact that the accelerations of the two bodies are related to each other.

The basic principle that we use in figuring this relationship out is that the length of the thread is conserved. Please refer to the figure beside to understand the explanation. Suppose that the mass

moves a length x along the inclined plane upwards. The moving pulley thus will descend a distance x. The length of the thread section AB now decreases by x. Thus, as seen in the figure A' B = AB-x. Since the length of the thread (AB + CD) has to be conserved, the length of the thread section CD must thus increases by x, C'D' = CD + x. In other words,

will descend a distance x relative to the moving pulley. Since the pulley itself has descended x, the total distance that

descends is x + x = 2x. To summarize, if

moves a distance x units

moves a distance 2x units. Thus, we have,