The cone, as it moves, undergoes rotation about two perpendicular axis as shown in the figure. One rotation is about the pivot and has a angular velocity magnitude of v/R directed upwards (perpendicular to the surface) - this is since the linear velocity is v and the radius of rotation is R.The second rotation vector is due to the cone's spinning about its axis passing through the apex. The radius of the base of the cone can be determined by trigonometry as
. The angular velocity of the cone about this axis is thus, 
. This problem is now similar to problem 1.55 - the case where the body was undergoing rotation simultaneously along two perpendicular directions.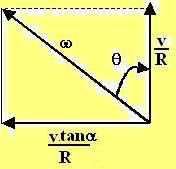
The magnitude of the net angular velocity and its angle to the normal can be determined from the figure below and are given by,
and the angle is given by,
No comments:
Post a Comment