 This is a particularly beautiful problem that I really loved solving in Irodov. This is one of the those rarely well crafted problems that simply makes you admire the man's ingenuity in creating problems. Enough of admiration (I could not help it) and now let's get down to the solution.
This is a particularly beautiful problem that I really loved solving in Irodov. This is one of the those rarely well crafted problems that simply makes you admire the man's ingenuity in creating problems. Enough of admiration (I could not help it) and now let's get down to the solution.Before I get into solving the problem lets gain some perspective. Let us start by considering a much simpler problem - a disc on an inclined plane as shown in the first figure. There are two forces acting on the disc in the direction perpendicular to the slope i) the component of gravity
 and ii) the normal reaction N. Since there is no component of acceleration for the disc along this direction and so we have,
and ii) the normal reaction N. Since there is no component of acceleration for the disc along this direction and so we have,
Along the direction of the slope there are two force acting, i) the component of force of gravity
 and ii) the force of friction f. Hence we have
and ii) the force of friction f. Hence we have
The interesting thing lies in understanding that when k the coefficient of friction is given by,

the force of friction acting on the disc is exactly equal in magnitude to the force of gravity pulling the disc down the slope. This critical value of friction if a disc were mere placed on the slope, the friction coefficient will be just sufficient to stop it from slipping. This is indicated from the fact the rate of change of velocity given by equation (0) is 0.
What happens to this disc if we impart if a velocity downwards on the slope? The disc will keep moving down the slope at a constant velocity.
What this Irodov problem attempts to investigate is to answer the question, "at this critical friction coefficient value, what if we impart an velocity side-wise rather than exactly down the slope?"
We shall now start to solve the original problem by considering a general version of the problem for a general value of k.
 The figure beside shows three views of the same figure to make things more clear. There are three forces acting on the disc at at given time, i) the force of gravity mg and ii) and the force of friction f and iii) the normal reaction N from the surface. The force of friction f always opposes the motion and hence acts in a direction that is exactly opposite to the velocity vector v. As the direction of the velocity of motion of the disc changes so does the direction of the force of friction so as to oppose it. This continually changing nature of the direction of the force of friction is what makes this problem so interesting.
The figure beside shows three views of the same figure to make things more clear. There are three forces acting on the disc at at given time, i) the force of gravity mg and ii) and the force of friction f and iii) the normal reaction N from the surface. The force of friction f always opposes the motion and hence acts in a direction that is exactly opposite to the velocity vector v. As the direction of the velocity of motion of the disc changes so does the direction of the force of friction so as to oppose it. This continually changing nature of the direction of the force of friction is what makes this problem so interesting.For this problem we have to consider forces in all three dimensions.
Forces along the direction normal to the inclined plane: There are only two forces acting in this direction as shown in the side view (middle picture) , i) the component of gravity
 and ii) the normal reaction N. There is no component of acceleration for the disc along this direction. So we have,
and ii) the normal reaction N. There is no component of acceleration for the disc along this direction. So we have,
Forces in the direction of the slope of the inclined plane: there are two forces acting this direction, i) the component of gravity
 and ii) the component of force of friction along this direction
and ii) the component of force of friction along this direction  . Let the acceleration of the disc in this direction be wx then we have,
. Let the acceleration of the disc in this direction be wx then we have,
Forces in the direction of 0 slope on the inclined plane : there is only one force acting in this direction namely the component of friction force
 . If the acceleration of the body is in this direction is wy then we have,
. If the acceleration of the body is in this direction is wy then we have,
In (4) and (5) the angle
 itself will keep changing and is unknown. But since this angle is the direction of the velocity vector of the disc and can computed from the relation,
itself will keep changing and is unknown. But since this angle is the direction of the velocity vector of the disc and can computed from the relation,
Now the trajectory of the disc can be calculated from (4), (5) and (6). Now I will simply collect (4), (5) and (6) in one place.

These are non-linear coupled differential equations with three variables and not amenable to an easy analytical solution. Since we have to ultimately determine a relation between v and
 it is better to derive our equations in terms of v rather than vx.
it is better to derive our equations in terms of v rather than vx.In the direction of the velocity vector we have:
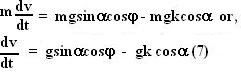
Also, from the basic geometry we know that,
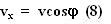
Thus we can rewrite the equation for dynamics of the body in terms of v, vx and
 as,
as,
Now that (4),(7),(8) represent the same motion of the body as do (4),(5),(6) only in terms of different variables. However, even this way of representation is not amenable to an easy general analytical solution for the system.
What simplifies the problem considerably is the fact that the we are operating at the cricital value of friction where the magnitude of force of friction is exactly equal to that of the component of gravity pulling it down the slope, ie.

that the problem specifies.
Applying this condition to (4) and (7) gives us,

(10),(11) reveal an interesting fact,

What this means is that the rate the absolute velocity of the disc decreases (due to the force of friction) the rate of change of the component of velocity of the body sliding downwards increases (due to gravity). Ultimately when the velocity vector aligns itself with the x-axis (direction of maximum slope) the force of friction will cancel out the force of gravity and keep slipping downwards at constant speed.
If the disc is imparted at an initial angle
 = 90 degrees, then initial value of vx will be 0 so from (12) we have,
= 90 degrees, then initial value of vx will be 0 so from (12) we have,
7 comments:
Thanks for the solutions. That you have given explanations for all solutions means that it is a great tool for students.
This is one of the best questions I liked in the basic laws of Mechanics.
I had a slightly different solution, though it finally follows Irodov's "Instruction" at the back of the book from some point on.
I use, dv/dt = (1/v)(a.v). Write v = v(cos(phi)i + sin(phi)j), and then the dot product reveals that a(tangential) = -a(x).
I think the key is that one should be quick to sight that the value of co-efficient of friction is tan(alpha). When it is given as one of the possible terms in an algebraic simplification, you should look out for it.
Your interpretation of its meaning is also much appreciated.
Thanks again!
I disagree with your point that the equations (4), (5), (6) have no easy analytical solution. Converting these into a differential equation between vy and phi (or vx and phi) leads to an integral of cosec(phi) which is ln(cosec(phi)-cot(phi)). Using this gives the value of v as desired. However, your solution (also Irodov's solution) is far more elegant.
thank u sir.
Absolutely beautiful solution.
Thanks.
Wonderful.
Thanks
I think other site proprietors should take this site as an model, very clean
and magnificent user genial style and design, as well as the
content. You are an expert in this topic!
Feel free to visit my weblog - the rain in spain dark tower
Greetings from Florida! I'm bored to tears at
work so I decided to browse your site on my iphone during lunch break. I enjoy the info you present here and can't wait to
take a look when I get home. I'm
shocked at how quick your blog loaded on my phone .. I'm not
even using WIFI,
just 3G .. Anyways, good site!
Also visit my website - Homepage
Post a Comment