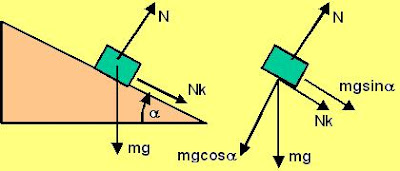
There are three forces acting on the mass, i) the force of gravity mg ii) the normal reaction N iii) force of friction Nk.
Along the normal direction to the inclined plane we have two forces N and
. The mass does not have any acceleration along this direction and so we have,
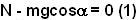
Along the horizontal place we have two forces, i) the force of friction Nk opposing the motion of the mass i.e. acting down the plane and ii) the component of force of gravity
. Let the deceleration of the mass along the plane be a and so we have,
We know from any standard physics textbook that,
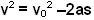
where v is the final velocity and s the distance traveled. When the mass stops, v=0 and so we have,
The work done by friction is simply the negative of the product of the force of friction and the distance traveled since they are in opposite directions and is given by,
2 comments:
can we solve the question by conservation of mechanical energy
Ofcourse Sanjay we can solve this using conservation of energy as well.
You must remember that friction also does work here and so some of the initial kinetic energy also goes into work done by friction.
Final kinetic energy (1/2 mv^2 ) = initial kinetic energy (1/2mvo^2) - potential energy gained (mgsin(alpha))- work done by friction (kmgcos(alpha)).
this will give exactly the same answer!!
Post a Comment