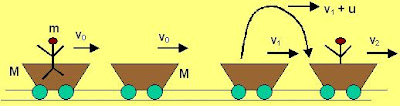
 Suppose that the final velocities of the rear and front buggies after jump became v1 and v2 respectively.
Suppose that the final velocities of the rear and front buggies after jump became v1 and v2 respectively.For the rear buggy, momentum before the jump is (M+m)v0. After the jump the rear buggy moves at v1 and so with a momentum Mv1. The person in the air moves with a velocity u relative to the rear buggy and so his velocity relative to a stationary observer is v1 + u. The momentum of the person in the air is thus m(v1+u). Since, there was no external force acting on the (rear buggy + man) system their total momentum must be conserved immediately before and after jump. This means that,

For the front buggy, the momentum of the (man + buggy) system just before and after he lands is conserved. Before he lands into the front buggy his momentum in the air is m(v1 + u) and the momentum of the buggy in front is Mv0 . After her lands, both the buggy and man move at a speed v2 together and so their combined momentum is (M+m)v2. In other words,

1 comment:
wow thnx a lot
Post a Comment