
Solution using Gauss Law:
Consider a Gaussian surface that is a spherical surface of radius r and passes through the point mass m. The reason for this choice of the Gaussian surface stems from an observation of the underlying symmetry in the problem. The reason for this choice is as follows:
The infinitesimally small area vector dA at any point on the surface of the spherical Gaussian surface will be aligned in the direction of the radius vector of this point (radially outwards). From the spherical symmetry of the problem it is also the magnitude of the gravitational flux vector
 (gravitational force per unit mass) , at all points on this Gaussian surface must be the same. Further, the direction of the gravitational flux at all these points must be directed radially inwards, in exactly the opposite direction of the area vector. Thus, the dot product
(gravitational force per unit mass) , at all points on this Gaussian surface must be the same. Further, the direction of the gravitational flux at all these points must be directed radially inwards, in exactly the opposite direction of the area vector. Thus, the dot product  .dA at any point on the sphere is simply
.dA at any point on the sphere is simply  da where
da where  and da are the magnitudes of the vectors
and da are the magnitudes of the vectors  and dA. This means that the surface integral can simply be evaluated as,
and dA. This means that the surface integral can simply be evaluated as,
This simplicity of evaluating the surface integral is the reason for this choice of the Gaussian surface.
Now from Gauss law,

Here M is the total mass contained within the Gaussian sphere and is equal to the mass of the sphere.
From (1) and (2) we have,

This means that force of gravity is exactly the same as if the sphere where to be treated as a point particle of mass M. Thus the gravitational potential energy will be given by

Solving the hard way:
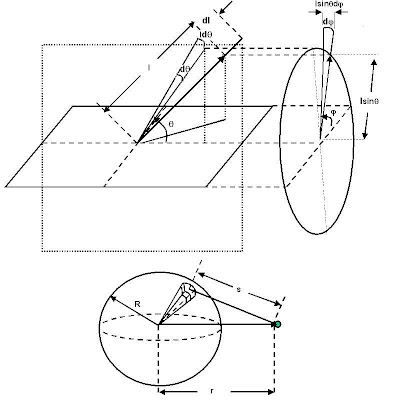
Consider an infinitesimally small piece of the sphere that is located at
 as shown in the figure . The mass of this infinitesimally small element will be
as shown in the figure . The mass of this infinitesimally small element will be
The gravitational potential energy of the point mass m due to this infinitesimally small piece of the sphere will be,

Here s can be determined by using the cosine rule in triangles,

The potential energy due to the entire sphere can be determined by integrating over the entire volume of the sphere,
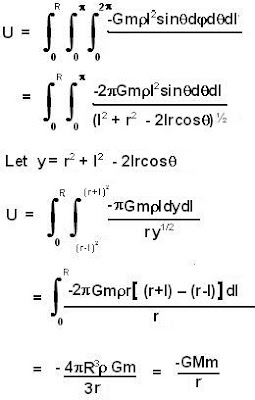
The force can be determined as,

No comments:
Post a Comment