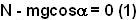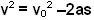Irodov Problem 1.137

Suppose we impart a velocity vo
at the bottom. As the particle moves up it gains potential energy and looses its kinetic energy i.e. velocity. Suppose that at the top-most point its velocity is v. By the time the particle reaches the top-most point it has gained a height of 2l and hence a potential energy of 2mgl. From conservation of energy we have,





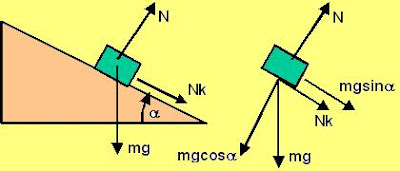
In order for the particle to complete the circle at no point during the particles motion there should be any slack in the string, i.e. it should be tense at all points.

There are two forces acting on the particle at the top-most point, i) the force of gravity mg and ii) the tension in the string both acting to pull the particle down. Since the particle is rotating in a circle of radius l , it is subject to a centripetal acceleration of . Hence we have,




The minimum value of vo corresponds to the case when at the top-most point the tension T is exactly 0, i.e. the particle just makes it in the loop. Substituting this condition we have,



From (3) and (1) we have,





When the particle is in the horizontal position its potential energy gained with respect to the lowermost position is mgl since its at a height l. Let its speed by v1 then we have,






At the horizontal position there is only one force acting in the horizontal direction - the tension in the string T. The particle is also subject to centripetal acceleration by the virtue of its motion in a circle of radius l. So we have,

Irodov Problem 1.136

As the mass slides down the slope it looses it potential energy and gains kinetic energy and so it velocity increases. At the base of the loop it has its maximum velocity. From this point its starts to climb up the loop and starts to loose its kinetic energy as it gains potential energy. When the particle is at an angle , as seen from the figure it will be at a height of from the ground. Let the speed of the particle be v at this point. Then the net change in potential energy must be equal to the particle's kinetic energy. At this point the particle has lost a height of and hence we have,






At this point there are two forces acting on the particle, i) the normal reaction from the surface N
and ii) the force of gravity mg. Since the particle is rotating in a circular path with radius h/2 it also experiences a centripetal acceleration of . Hence along the direction perpendicular to the surface we have,





At the point when the mass looses contact with the surface, the normal reaction becomes zero, i.e. N=0. Using this condition in (1) and (2) we have,







At this point we can use (1) to compute the velocity of the particle as,




AT this point however, the particles velocity is directed along the slope of the circular surface. The horizontal component of the particle is then given by

Irodov Problem 1.135

The total potential energy lost by the disc just before it leaves the surface is given by mg(H-h). This is converted into the discs kinetic energy and so if its horizontal launch velocity off the hill is given by,




The time t the disc takes before it hits the floor since it launches off is given by,





The horizontal distance traveled during this time is given by,



This is maximized when the first derivative dx/dh=0 and the second derivative is negative. It is trivial to see that this occurs at h = H/2 and the corresponding maximum distance traveled will be H.

Irodov Problem 1.134

There are three forces acting on the mass, i) the force of gravity mg ii) the normal reaction N iii) force of friction Nk.

Along the normal direction to the inclined plane we have two forces N and
. The mass does not have any acceleration along this direction and so we have,



Along the horizontal place we have two forces, i) the force of friction Nk opposing the motion of the mass i.e. acting down the plane and ii) the component of force of gravity . Let the deceleration of the mass along the plane be a and so we have,





We know from any standard physics textbook that,



where v is the final velocity and s the distance traveled. When the mass stops, v=0 and so we have,






The work done by friction is simply the negative of the product of the force of friction and the distance traveled since they are in opposite directions and is given by,

Irodov Problem 1.133

Force is the negative gradient of potential i.e. in catersian coordinates we have,

.

In this problem the question is whether or not there exists some potential function U whose negative gradient is the force F.

a) From the problem we have,







From (1b) and (1c) it is clear that U = f(x) i.e. U is only a function of x and not of y and z. If however, this were true then, (1a) is impossible since it implies that U is of the form U = axy + f1(y,z). This contradiction implies that F cannot be a potential function.

b)From the problem we have,







From (2c) clearly U = f(x,y). From (2a), we have that the potential U has the form . From (2c) the potential can be written as . Based on these observation we can see that a potential function that satisfies all above conditions is,
.


In other words there is a potential function that can result in the above force.