Let the mass per unit length of the falling chain be 
. The mass of an infinitesimally piece of chain of length dl is then given by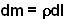
. The momentum imparted by a piece of chain that is dl long and that hits the table with a speed v is given by
.If this infinitesimally small piece of chain of length dl falls in time dt, the instantaneous force imparted by it (force is change in momentum per time) on the table at a speed v is given by,
. After a time t has elapsed since the chain starts to fall, the velocity of the tip of the chain that is hitting the table will be v=gt since it has been falling under the influence of gravity. This means that the force exerted by the falling chain as a function of time t will be 
.In time t since the chain starts to fall, a length of
would have fallen on the table (since it is freely falling under gravity). This means that after a time t has elapsed since the chain starts to fall the mass that lies on the table would be 
. The force exerted by this part of the chain would then be 
. Clearly this is half of the force exetrted by the falling chain.
No comments:
Post a Comment