Irodov Problem 1.53

(a) The velocities at the three points A,B and C are illustrated in the figure beside. At each of these points the net velocity vector is the sum of two vectors i) the linear motion of the ball and ii) the rotational velocity along the rim. The magnitude of both these vectors will be v, since the ball is not slipping. The direction of the velocity vector will always be at a tangent to the rotating circle, whereas the linear velocity vector will be directed along the direction of linear motion.





(b)
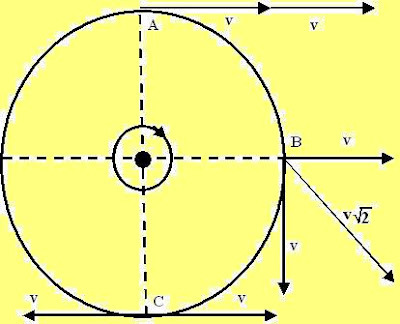
Every point on the ball experiences three different kinds of acceleration components, i) centripetal acceleration directed towards the center of the ball, ii) tangential rotational acceleration w directed along the tangent to the surface of the ball and iii) the linear acceleration w due to the linear motion of the ball.
The net acceleration at any point is thus the sum of all these three vectors. Now we can find the accelerations at the asked points on the balls as,