We can solve this problem in two ways, completely mathematically or with our knowledge of centripetal acceleration.Solution with the knowledge of centripetal acceleration: We know from previous problems that the radial acceleration experienced by points A and B will be
(see problem 1.52 for a better explanation). Here, v is the linear velocity of the cylinder (velocity of the axis passing through its center) as it rolls. We, however also know that the radial acceleration of a point must be equal
to where, 
is the instantaneous tangential velocity of the point and the instantaneous radius of curvature of the trajectory of the point is 
. The figure depicts the instantaneous tangential velocities experienced by the points A and B and the radial accelerations. The instantaneous tangential velocity vector at any point in the cylinder's rim is the sum of two velocity vectors i) due to the linear motion of the cylinder and ii) the rotational velocity of the cylinder (in the direction of the tangent) both with the same magnitude v. (a) For point A thus,
For A, as seen from the figure,
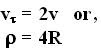
(b) For point B, the tangential velocity vector is oriented at 45 degrees to the vertical as seen in the figure. The radial vector for acceleration is also oriented at 45 degrees to the vertical. The component of centripetal acceleration along the radial direction is given by,
Solution based on purely mathematical treatment:
We know that the radius of curvature is given by, here x' and x'' represent the first and second derivatives with respect to time and the same for y.
(why? see here for the explanation).(a) Based on the figure we know that,
(b) Similarly using the figure we can write,
Of course using the formula seems simpler, but I wanted show how we can use both the concepts.
No comments:
Post a Comment