

Figure shows an typical instantaneous state of the two particles during their motion as particle B is continuously aimed towards particle A. Let x be the horizontal distance between the two particles and y be the vertical distance between the two particles. From figure 2 we can write the motion of the particle B given by the following equations,
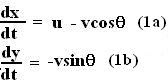
Now, integrating both side of (1a) from the t=0 to the time when A and B meet we obtain,

The integral is from 0 to 0 in the above equation because the horizontal distance between A and B initially is 0 and finally when they meet also it will again be 0. This can seen from the figure, from the definition of x - as the horizontal distance between A and B.
 In the figure, we resolve all velocities along and perpendicular to the line connecting the two bodies.
In the figure, we resolve all velocities along and perpendicular to the line connecting the two bodies.
If r is the distance between the two bodies then, as seen from the figure r decreases as at any given instant of time. Thus,
at any given instant of time. Thus,
The same result can of course also be derived by transforming (1a,1b) to polar coordinates. Now if r is the vector connecting particles A and B then,
Using (4) can rewrite (1a,1b) as,


Integrating both side of (3), it would mean that,

Now we can use (2) to solve for from (5) as,
from (5) as,

 In the figure, we resolve all velocities along and perpendicular to the line connecting the two bodies.
In the figure, we resolve all velocities along and perpendicular to the line connecting the two bodies.If r is the distance between the two bodies then, as seen from the figure r decreases as
 at any given instant of time. Thus,
at any given instant of time. Thus,
The same result can of course also be derived by transforming (1a,1b) to polar coordinates. Now if r is the vector connecting particles A and B then,

Using (4) can rewrite (1a,1b) as,


Integrating both side of (3), it would mean that,

Now we can use (2) to solve for
 from (5) as,
from (5) as,
4 comments:
Hello there! I've been busying myself for the last two days in trying to find the trajectory of the particle with velocity v in the reference frame of the particle with velocity u. The resut is that I end up with a non-linear trignometric second order differential equation and I can't seem to find a satisfactory solution even if I try to solve it with software such as Maple. My idea was that if I find the law of motion in the said reference frame, the time of intersection will be equal with the time it takes for the radius vector to have it's projection on the x axis equal to l. Do you think it it solvable, or should I try a different aproach? Thank you very much,
Alexandru
As seen from the frame fixed to the particle moving horizontally (moving with velocity u), the motion of the particle with velocity v is given by eqns 1a and 1b but with the signs reversed.
Indeed the equations are rather non-linearly coupled due to the trigonometric relationships. Consequently, I am not sure if it is easy to find a nice closed form solution for the tragectory in cartesian coordinates. I will try and see if I can do this and get back to you if I can.
That's the reason you have to use the trick of using both polar and cartesian coordinate systems to solve the problem. You first obtain (2) using cartesian coordinates and then use polar coordinates to solve the problem using (3).
Well, I've finally managed to solve it with your method transposed in the reference frame fiex to the particle with velocity u. The shole difference was that the trigonometric time integral was of a sin function, not cosin. Anyway I'm not particulary satisfied, I wanted to find the trajectory of the particle with velocity v, but I have a lot of problems to solve and a lot of theory to study so I must go on. Thanks for posting these solutions here, it would have been painful to simply skip the problem.
thankyou.............. you are doing a great job..........!!!!!!!!!!!!.......
Post a Comment