Irodov Problem 1.92

First let us consider an infinitesimally small part of the chain that spans angle of and suppose that the tension in the string is T, as shown in the figure beside (top view - as if seeing from the top of the cone; the plane of the figure is a horizontal plane cutting the cone). This means that the rest of the chain will be pulling this piece of chain with a force T from both its ends. The direction of this force will be along the tangent of the chain as shown in the figure. The net force this piece of chain exerts on the cone will be the sum of the components of the forces on its two ends along a direction radially inwards equal to (see here for the behaviour of the sine function as the angle tends to zero).

Now let us consider the force diagram of the infinitesimally small chain piece. Let the mass of this chain piece be dm, then clearly since the entire mass m is distributed evenly over the entire 360 degrees, we have,




Let dN be the normal reaction offered by the cone on the infinitesimally small chain piece. There are three forces acting on the chain piece, i) the force of gravity (dm)g, ii) the normal reaction dN and iii) the force net force exerted by the rest of the chain of this piece due to the tension given by as derived at the beginning of the solution. The chain piece is also subject to centripetal acceleration of magnitude 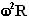directed towards the center due to its rotation with the cone The force diagram is shown beside.

Force equation along the vertical direction :
Since the chain piece has no acceleration along this direction, the only two forces are the component of the normal reaction and the force of gravity. Hence we have,




Force equations along the horizontal direction (radial direction):
The are two forces acting along this direction, i) the component of the normal reaction and ii) the tension force exerted by rest of the chain onto this small piece given by . The chain piece is accelerating radially inwards at 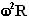. Thus we have,