Irodov Problem 1.85

The speed of the sphere at a given angle can be determined by the fact the total energy of the system will be conserved.
The potential energy lost will be 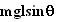and this will be converted to the kinetic energy of the sphere given by . In other words,






(a) There are two components of acceleration that the sphere is subject to i) the centripetal acceleration acting radially inwards (towards the pivot) and ii) the tangential acceleration (since the body is not only rotating but also increasing in speed as it moves) .















(3) is not surprising since the only force acting in the tangential direction is the component of gravity given by and thus the acceleration will be . The net acceleration is the Euclidean norm of the tangential and radial accelerations given by,


There are two forces acting on the mass along the radial direction, i) the tension T acting radially inwards and ii) force of gravity acting vertically downwards . The radial acceleration of the mass is directed radially inwards. Thus, we have,



(b) The vertical component of the sphere's velocity is given by as shown in the figure. At its maxima, the first derivative is 0 and the second derivative is negative.








As seen from (6) the second derivative will be negative when (5) is satisfied. The tension at this angle can be calculated using (4) and is given by,





(c)
When the vertical component is 0,