Let us suppose the spring constant of the spring is 
. The tension in the spring when the spring is stretched by a length x is given by 
.Let us first consider the mass m2. There are four forces acting on this mass, i) the force of gravity m2g, ii) the normal reaction from the surface N2 iii) the force of friction opposing its motion f2 and iv) the tension in the spring pulling it
. Before this mass starts to move there is no acceleration in any direction and so we have,
m2 will break free when f2 attains its maximum possible value i.e. N2k = m2gk. In other words we have for breaking condition,
Now let us consider the mass m1. There are five forces acting on it at any given time, i) the force of gravity m1g, ii) the normal reaction from the surface N1 iii) the force of friction opposing its motion f1 , iv) the tension in the spring pulling it
and v) the external force F. The spring can only extend if the friction force f1 has already attained its maximum possible value and can no longer resist the force. In other words,
Considering the forces acting on the mass in the vertical direction and since there is not acceleration in this direction, we have,
In other words,
As soon as the mass m1 breaks free under the force F it will start to accelerate. Suppose at any instant its speed is v as shown in the figure. Then we have,
If you notice (7) is actually nothing but the conservation of energy equation, the total work done by all the forces on the mass m1 gets converted into its kinetic energy. Instead of writing it down, I derived it just to show how it actually originates.
The maximum possible extension of the spring will occur when the mass m1 can no longer move to the left and starts to move back to the right due to the action of the spring. At this point v=0. For the minimum possible value of F this extension will be just sufficient to break m2 free.
From (7) we have,
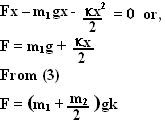
Last but not the least, thanks to Nalin for showing me the crucial insight into the problem.
6 comments:
thanx for giving such a clear cut explanation... i had doubt in this Q.no. 1.123.... thank you once again.. i am preparing for this year's jee n i also like solving irodov.. will you mind giving me your e-mail id so that i can ask you my doubts ???? PLEEEASE... my mail id is..... skygirl.sengupta@gmail.com.. i will wait for your reply..
dear skygirl.sengupta,
please email me at irodov.solutions@gmail.com
I do this just as a hobby in my spare time and my job keeps me busy. So please bear with me if you get your answers a bit delayed.
thank you sir
thanks sir,my attemps at jee have been finished,but still i love to do physics,i am at nit-k,i had doubt in this problem,but now (after reading your solution)my concept regarding spring block problem has strengthened,thank you once again.
thanks sir,my attemps at jee have been finished,but still i love to do physics,i am at nit-k,i had doubt in this problem,but now (after reading your solution)my concept regarding spring block problem has strengthened,thank you once again.
sir
truly telling you i was too afraid to solve irodov due to the hoax "it is too hard" but after i seeked some solutions from you im very well capable of solving them.
thank you
Post a Comment